10.4 Matched or Paired Samples
DEPENDENT SAMPLES
If the choice of a sample member in one group automatically determines who's going to be selected from the second group, then the samples are dependent. In these samples, there's a distinct connection between members of the two samples. For example, when samples are taken from the same group at two different points in time (such as pre and post results) or under two different conditions (such as testing alone vs with a proctor), the two samples will be dependent. The group members can be different people and yet result in dependent samples if there is a natural connection between sample members from those two groups such as spouse/partner, twins, or some predefined criteria (gender, lifestyle, age, etc.) that can be used to match a member from one sample to another.
The requirements for hypothesis testing with dependent samples are:
- Samples taken are simple random samples with observations that are independent within each group. Sample sizes are often small.
- The two measurements (samples) are drawn from the same or same pair of individuals or objects (population variances should be the same)
- Either the matched pairs have differences that come from a population that is normal or the sampled number of differences is sufficiently large so that distribution of the sample mean of differences is approximately normal.
If the above conditions hold, then we can use the sampling distribution of the mean of the differences between matched pairs in the sample, [latex]\bar d[/latex], to conduct our hypothesis test. Since the differences form just one list of values, we'll perform a t-test. The test statistic for the dependent t-test is \[t = \frac{\bar d}{s_{\bar d}}\]
where [latex]\bar d[/latex] is the mean difference and [latex]s_{\bar d}[/latex] is the standard error of the mean difference, which is
\[s_{\bar d} = {s_d\over\sqrt{n}}\]where [latex]s_d[/latex] is the standard deviation of the differences of the data values from [latex]n[/latex] matched pairs in the samples.
Symbols Used in Hypothesis Testing for Means
| Sample Statistic | Population Parameter | |
| Mean | [latex]\bar x[/latex] | [latex]\mu[/latex] |
| Difference in Two Means (Independent) | [latex]\bar x_1 - \bar x_2[/latex] | [latex]\mu_1-\mu_2[/latex] |
| Difference in Two Means (Dependent) | [latex]\bar d[/latex] | [latex]\mu_d[/latex] |
Here's an overview of testing with dependent samples.
Practice
WORKED OUT EXAMPLE - Dependent Samples
A local group of economists wants to study the effects of the pandemic on the small businesses in their city. A survey was sent out to a random sample of small businesses to anonymously report their weekly earnings for January of 2020 and a year later in January 2021. Assume that the weekly earnings are normally distributed. Only 10 businesses provided enough data as shown below. Data values are in thousands.
| January 2020 | 87.7 | 54.1 | 32.5 | 85.8 | 33.7 | 77.8 | 70.6 | 70.4 | 104.8 | 63.1 |
| January 2021 | 74.3 | 46 | 53.4 | 78.8 | 44.1 | 64.4 | 63.6 | 67.9 | 75.2 | 48 |
Use [latex]\alpha = 0.01[/latex] to decide whether there is sufficient evidence to support that the pandemic reduced average weekly earnings for small businesses.
SHOW SOLUTION
Independent or dependent samples?
We might be tempted to compare the average earnings of all of the small businesses in January 2020 with the average of all small businesses in 2021, that is, to test if the difference of averages is [latex]\mu_1<\mu_2[/latex], but that will fail to capture the information contained in the pairings. If January 2021 earnings deviate from January 2020 earnings in both directions (some are lower, some higher), it can lead to a situation where the two averages seem equal. Therefore, if we focus instead on the pairwise differences between samples, we will have a set of data values of differences and since each observation within group is independent, we can then proceed with a one sample t-test. In the example above, if January 2021 earnings are lower, then we'd expect the difference between January 2020 and January 2021 earnings to be positive. Note that if instead you were to look at it the other way around, the difference in earnings between January 2021 and January 2020, then the difference would be negative if January 2021 earnings are lower. So, what we'll need to do is pick which way we're going to compute the difference and proceed from there. The null hypothesis will be that on average these differences will amount to zero, which is to say that there's really not a whole lot of difference between the two groups. The average of the differences from our samples is [latex]\bar d[/latex]. Let's find that next by first finding the difference between January 2020 and January 2021 earnings for each pair:
The null hypothesis will be that on average these differences will amount to zero, which is to say that there's really not a whole lot of difference between the two groups. The average of the differences from our samples is [latex]\bar d[/latex]. Let's find that next by first finding the difference between January 2020 and January 2021 earnings for each pair:
| January 2020 | 87.7 | 54.1 | 32.5 | 85.8 | 33.7 | 77.8 | 70.6 | 70.4 | 104.8 | 63.1 |
| January 2021 | 74.3 | 46 | 53.4 | 78.8 | 44.1 | 64.4 | 63.6 | 67.9 | 75.2 | 48 |
| DIFFERENCE | 13.4 | 8.1 | -20.9 | 7 | -10.4 | 13.4 | 7 | 2.5 | 29.6 | 15.1 |
|---|
For the differences we can calculate their average and standard deviation by using a calculator (One Variable Statistics calculator at SUBEDI Calcs, for example).
The average of the differences, [latex]\bar d=6.48[/latex]. This is our sample statistic.
The standard deviation of the differences, [latex]s_d = 13.977028773431545[/latex].
In order to understand how usual or unusual this sample is, we need to know the sampling distribution of [latex]\bar d[/latex]. This [latex]\bar d[/latex] will be an estimate for the actual difference between the two populations, [latex]d[/latex]. On average, if we expect the January 2021 earnings to be lower, then we'd expect the average of the differences to be positive (if we compute differences between 2020 and 2021 for the same month of January: 2020 Earnings - 2021 Earnings. So the claim we would like to test is if, on average, the difference of January 2020 and January 2021 earnings is positive. This claim in symbols is: [latex]\mu_d > 0[/latex]. The opposite of this claim is [latex]\mu_d\le 0[/latex].
Since the differences are just one data list, we will use one sample t-test with data option to perform a t-test with the differences between the samples data calculated earlier (last row in the table above). However, if we're using one of the calculators below, we can actually skip the step to calculate the differences. We only have to enter the data from each samples into the appropriate input boxes and enter a few other details about the test so that calculator can give us the correct results.
Sample information
Sample data is paired difference in the sample.
STEP 1: Write the claim (or what's being tested) using mathematical symbols
On average the differences are positive. That is, [latex]\mu_d > 0[/latex].
STEP 2: Write the opposite of the claim using mathematical symbols
Opposite of the claim: [latex]\mu_d\le 0[/latex].
STEP 3: Write the null and alternative hypothesis
The null hypothesis is the statement that contains the condition of equality which in this case is the opposite of the claim
| [latex]H_0:\mu_d \le 0[/latex] [latex]H_a:\mu_d > 0[/latex] |
OR | [latex]H_0:\mu_d = 0[/latex] [latex]H_a:\mu_d > 0[/latex] |
STEP 4: Identify the tail-type of the test and the level of significance, [latex]\alpha[/latex]. If [latex]\alpha[/latex] is not given, assume it to be 5% or 0.05.
This is a right tailed test. Why?
Since the level of significance is given, use that value of [latex]\alpha=0.01[/latex] (or 1% level of significance)
STEP 5: Check if CLT conditions are valid.
The number of paired sample is small, lower than 30, so we need the paired differences in the population to be normally distributed to meet CLT conditions. We'll perform a t-test for dependent means since the population standard deviation of the paired differences in the population is not known.
This is the stage where we assume the equality in the null hypothesis is true, that is, assume [latex]\mu_d=0[/latex]. We're assuming that there's no change between the weekly earnings for small businesses in January of 2020 and January of 2021. We know that the sampling distribution of the mean of the paired difference, [latex]\bar d[/latex], will be approximately normally distributed with mean of [latex]\mu_{\bar d} = 0[/latex] and a standard deviation of [latex]\sigma_{\bar d} = \dfrac{\sigma_d}{\sqrt n}[/latex]. Since the population standard deviation of [latex]\sigma_d[/latex] is unknown, the standard deviation of the sampling distribution of [latex]\bar d[/latex] can be approximated as [latex]\sigma_{\bar d} \approx s_{\bar d}=\dfrac{s_d}{\sqrt n}[/latex] [1]. This sampling distribution can be approximated by a t-distribution with [latex]n-1[/latex] degrees of freedom, where n is the number of matched pairs.
Results from STEP 6 can be obtained using a calculator. See below.
STEP 6: Plot t-score and find the p-value.
Degrees of freedom for t-test: [latex]df = n - 1 = 10 - 1 = 9[/latex].
Difference of the matched pairs has an average of [latex]\bar d = 6.48[/latex]. The standard error of the sampling distribution can be approximated by \[s_{\bar d}=\dfrac{s_d}{\sqrt{n}} = \dfrac{13.977028773431545}{\sqrt{10}}=4.41992458458\]
The t-score (test statistic) is: \[\dfrac{\bar d - \mu_d}{s_{\bar d}}=\dfrac{6.48 - 0}{4.41992458458}=1.46608836328\]
The p-value is the area to the right of this test statistic.
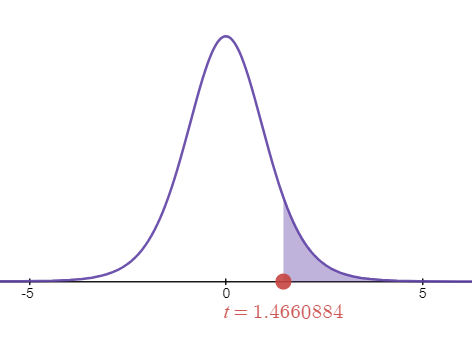
t-test statistic is plotted on the graph above. Since the test is right-tailed, the p-value is the area to the tail from test statistic, shaded in purple on the graph above. Let's take a look at how to calculate p-value, using calculators.
Calculate p-value
Use one or more of the calculators below to calculate p-value.
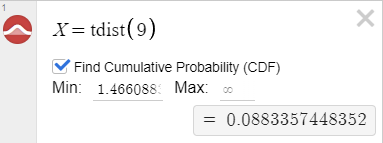
Desmos
✅ Find cumulative Probability (CDF)
Min: 1.46608836328 Max: [latex]\infty[/latex] (leave blank for [latex]\infty[/latex])
p-value = 0.0883357448358
StatKey
1) Enter degrees of freedom, df
2) Select Right Tail checkbox on the top left of the graph
3) Change the value to that of our test statistic, t = 1.466 (3 decimal places)
4) The value shown in the area/proportion box at this stage is the p-value
Ti-83/84+
Enter the following, select Paste and press the ENTER button twice.
lower: 1.46608836328
upper: 10^99
df: 9
Paste
STEP 6: Using Online Calculator (Recommended)
SUBEDI Calculator
Go to Inference for the Mean @ rsubedi.com
Input Type
Number of Samples
Independent or dependent samples?
Distribution Type for Test
Alternative Hypothesis
Confidence Interval? ← Optional
Enter Sample Data
Enter your data for the two samples in the spreadsheet columns shown for data entry. You do not need to enter the difference data as the calculator will automatically calculate that to arrive at the test results. You can copy your data from the original source (comma or separated list, spreadsheet data, etc.) and paste that into the table on the calculator.
CALCULATE
Results show in a panel to the right. Test statistic t, p-value, and df are displayed. The spreadsheet displays an additional column for the pair-wise difference of the sample data
LibreText Calculator
Go to: Two Dependent Samples With Data from the list of online calculators
Enter the following values and press Calculate.
| Data 1:
Enter Your Comma-Separated Data Values
|
|||
| Data 2:
Enter Your Comma-Separated Data Values
|
|
⭕[latex]\quad\lt[/latex]
🔘[latex]\quad\gt[/latex]
⭕[latex]\quad\ne[/latex]
|
CL (confidence level) You can ignore CL entry |
CALCULATE
Results displayed are:
[latex]p[/latex]: p-valueData Diff displayed at the bottom of the results shows the differences between pairs. Ignore LB and UB, if you did not enter confidence level.
STEP 7: Make the decision by comparing p-value with α
p-value is 0.0883357448358 which is more than [latex]\alpha[/latex] of 1%. Since p-value is more than [latex]\alpha[/latex], we fail to reject the null hypothesis ⇒ There's not enough evidence to support Ha.
STEP 8: Interpret your decision in the context of original claim
There is insufficient evidence at a significance level of 1% to support that the pandemic reduced average weekly earnings for small businesses.
Practice

