10.3 Comparing Two Independent Population Proportions
HYPOTHESIS TESTING FOR DIFFERENCE BETWEEN PROPORTIONS WITH TWO SAMPLES
When testing about claims that compare two groups (populations), we'll need to obtain samples from each group to test those claims. Typically studies comparing two groups (such as the treatment and control groups in experiments/clinical trials or a company claiming that its brand has more market share than its competitors, etc.) will require us to obtain sample from each group and use the difference between the two groups to test claim made about those populations.
Independent Samples: Two samples are independent if the selection of sample members from one population does not in any way affects the selection of sample members in the second population.
We'll focus only on independent samples in this unit.
All of hypothesis testing for proportions with two samples will fall into one of the following scenario:
| SCENARIO 1 |
SCENARIO 2 |
|||||
| [latex]H_0:p_1\ge p_2[/latex] [latex]H_a:p_1 < p_2[/latex] |
OR | [latex]H_0:p_1-p_2 \ge 0[/latex] [latex]H_a:p_1-p_2 < 0[/latex] |
[latex]H_0:p_1\le p_2[/latex] [latex]H_a:p_1 > p_2[/latex] |
OR | [latex]H_0:p_1-p_2 \le 0[/latex] [latex]H_a:p_1-p_2 > 0[/latex] |
|
| SCENARIO 3 | ||||||
| [latex]H_0:p_1 = p_2[/latex] [latex]H_a:p_1 \ne p_2[/latex] |
OR | [latex]H_0:p_1-p_2 = 0[/latex] [latex]H_a:p_1-p_2 \ne 0[/latex] |
||||
Note that for scenarios 1 and 2, the null hypothesis may be written with [latex]=[/latex] sign instead of [latex]\ge[/latex] or [latex]\le[/latex].
When conducting a hypothesis test that compares two independent population proportions, the following characteristics should be present:
- The two independent samples are simple random samples that are independent.
- The number of successes is at least five, and the number of failures is at least five, for each of the samples.
- Growing literature states that the population must be at least ten or 20 times the size of the sample. This keeps each population from being over-sampled and causing incorrect results.
Comparing two proportions, like comparing two means, is common. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions.
Comparing two proportions, like comparing two means, is common. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions.
The difference of two proportions follows an approximate normal distribution that is centered at [latex]p_1 - p_2[/latex] with a standard error of \[\sqrt{p_c(1-p_c) \left( {1\over n_1} + {1\over n_2} \right)}\]Generally, the null hypothesis states that the two proportions are the same. That is [latex]H_0:p_1 = p_2[/latex] . Recall that we start hypothesis testing by assuming the equality in the null hypothesis is true. In this case, we're assuming that [latex]p_1 = p_2[/latex], which means that the two population proportions are the same (no difference). With no difference between the population proportion, we can compute the pooled proportions, \[p_c={{x_1+x_2}\over{n_1+n_2}}\] and the test statistic is:\[z=\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{p_c(1-p_c) \left( \frac{1}{n_1} + \frac{1}{n_2} \right)} }\]
These formulas for two sample test for the difference of proportions are shown here so that you can recognize them for what they are but when conducting two sample tests, we'll be using calculators to speed up our calculations so that you won't have to remember these formulas.
Symbols Used in Hypothesis Testing for Proportions.
| Sample Statistic | Population Parameter | |
| Proportion | [latex]\hat p[/latex] | [latex]p[/latex] |
| Difference in Two Proportions | [latex]\hat p_1 - \hat p_2[/latex] | [latex]p_1-p_2[/latex] |
EXAMPLE
A new beta-blocker medication is being tested to treat high blood pressure. Subjects with high blood pressure volunteered to take part in the experiment. 240 subjects were randomly chosen to receive the medicine and 170 received a placebo. Blood pressure was lowered to healthy levels in 126 of the treatment group and 80 of the controls. Test the claim that the new beta-blocker medicine is effective at a significance level of [latex]\alpha = 0.05[/latex].
SHOW SOLUTION
How can we tell?
There are two groups (or populations) that we are comparing here-- the treatment (those receiving the new beta-blocker) and the placebo (control) groups. We're testing to see if the new beta-blocker is effective. In order to do so, we'll compare the percentage of people who improve between the groups. Since we're dealing with precents (or proportions), this test is going to be about proportions (more precisely the difference between population proportions).
Let's label the treatment population as group 1 and the placebo as group 2.
[latex]p_1 =[/latex] the proportion of subjects showing improvement in the treatment group
[latex]p_2 =[/latex] the proportion of subjects showing improvement in the placebo group
Sample information
Treatment Group:
Sample size, [latex]n_1=240[/latex];
Number of successes, [latex]x_1=126[/latex];
Sample proportion, [latex]\hat p_1=\dfrac{126}{240} = 0.525[/latex]
Placebo (Control) Group:
Sample size, [latex]n_2=170[/latex] ;
Number of successes, [latex]x_2=80[/latex];
Sample proportion, [latex]\hat p_2=\dfrac{80}{170} = 0.470588235294[/latex]
STEP 1: Write the claim (or what's being tested) using mathematical symbols
The claim we're testing is that new beta-blocker medicine is effective. If the beta-blocker treatment is effective, we'll see that the proportion of subjects who show improvements will be higher in the treatment group than the placebo group. That is, [latex]p_1 > p_2[/latex].
STEP 2: Write the opposite of the claim using mathematical symbols
Opposite of the claim: Opposite of the claim: [latex]p_1\le p_2[/latex]
STEP 3: Write the null and alternative hypothesis
The null hypothesis is the statement that contains the condition of equality which in this case is the opposite of the claim
| [latex]H_0: p_1\le p_2[/latex] [latex]H_a: p_1 > p_2[/latex] |
OR | [latex]H_0: p_1 = p_2[/latex] [latex]H_a: p_1 > p_2[/latex] |
STEP 4: Identify the tail-type of the test and the level of significance, α. If α is not given, assume it to be 5% or 0.05.
This is a right tailed test. Why?
Since the level of significance is given: [latex]\alpha = 0.01[/latex] (or 1% level of significance)
STEP 5: Check if CLT conditions are valid: [latex]np > 5[/latex] and [latex]nq > 5[/latex].
Treatment group: [latex]n_1 p_1 > 5[/latex] and [latex]n_1 q_1 > 5[/latex]. Placebo group: [latex]n_2 p_2 > 5[/latex] and [latex]n_2 q_2 > 5[/latex]. This is the stage where we assume the equality in the null hypothesis is true, that is, assume [latex]p_1=p_2[/latex]. We're assuming that there's no difference between the treatment and placebo groups, that is, we're assuming the medicine doesn't work (makes no difference). However, unlike in the case of one sample tests, this null assumption doesn't give us the values of [latex]p_1[/latex] and [latex]p_2[/latex] that we can use to test if the CLT conditions are met. However, since we're assuming that the two proportions are the same, we can use both samples to estimate the pooled proportion, [latex]p_c[/latex]. \[p_c=\frac{x_1+x_2}{n_1+n_2}=\frac{126+80}{240+170}=0.50243902439.\]
Wel'll use this value of [latex]p_c[/latex] to check the CLT conditions. Note that [latex]q_c = 1 - p_c[/latex]. [latex]n_1 p_c = (240)(0.50243902439) = 120.585365854[/latex] and [latex]n_1 q_c = (240)(1- 0.50243902439) = 119.414634146[/latex].[latex]n_2 p_c = (170)(0.50243902439) = 85.4146341463[/latex] and [latex]n_2 q_c = (170)(1 - 0.50243902439) = 84.5853658537[/latex]
Since all quantities are more than 5, we know that the sampling distribution of the difference of sample proportions will be approximately normally distributed with mean of [latex]\mu_{\hat p_1 - \hat p_2} = p_1-p_2=0[/latex] µp̂1–p̂2 = p1 – p2 = 0 and standard deviation (also known as standard error) of [latex]\sigma_{\hat p_1 - \hat p_2}[/latex].
\[\mu_{\hat p_1 - \hat p_2}=0\]\[\sigma_{\hat p_1 - \hat p_2} = \sqrt{p_c(1-p_c)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)} =\sqrt{0.50243902439(1-0.50243902439)\left(\frac{1}{240}+\frac{1}{170}\right)}=0.0501218028601\]
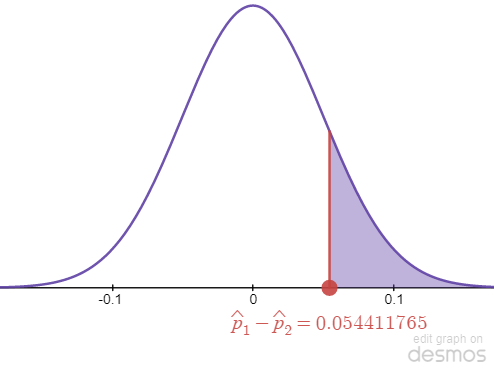
STEP 6: Plot [latex]\hat p[/latex] and find the p-value.
[latex]\hat p_1 - \hat p_2[/latex] is plotted on the graph above. Since the test is right-tailed, the p-value is the area to the tail from [latex]\hat p_1 - \hat p_2[/latex], shaded in purple on the graph above. To find the p-value, we can use one of the following methods:
DESMOS
✅ Find cumulative Probability (CDF)
Min: 0.0544117647059 Max: [latex]\infty[/latex] (leave blank for [latex]\infty[/latex])
STATKEY
1) Click on Edit parameters on the right and enter the mean as 0 and standard deviation as 0.0501218028601
2) Select Right Tail checkbox on the top left of the graph
3) Change the value to that of our sample statistic, [latex]\hat p_1 - \hat p_2[/latex] = 0.054 (3 decimal places)
4) The value shown in the area/proportion box at this stage is the p-value
Ti-83/84+
Enter the following, select Paste and press the ENTER button twice.
lower: 0.0544117647059
upper: 10^99
µ: 0
σ: 0.0501218028601
Paste
STEP 7: Make the decision by comparing p-value with α
p-value is 0.138830050765 which is greater than α of 5%. Since p-value is greater than α, we fail to reject the null hypothesis ⇒ There's not enough evidence to support Ha.
STEP 8: Interpret your decision in the context of original claim
There is insufficient evidence to support the claim that the new medicine is effective at a significance level of 0.05.
ONLINE CALCULATOR Approach
SUBEDI Calculator
Go to Inference for the Proportion @ rsubedi.com
Number of Samples:
🔲 ONE SAMPLE ✅ TWO SAMPLES
Alternative Hypothesis:
🔲[latex]\quad\lt[/latex] ✅[latex]\quad\gt[/latex] 🔲[latex]\quad\ne[/latex]
Confidence Interval? ← Optional
🔲 Include
Sample Statistics Information:
✅ Successes 🔲 [latex]\hat p[/latex] (p-hats)
Sample Size, [latex]n_1[/latex]: Successes, [latex]x_1[/latex]
240 126
Sample Size, [latex]n_2[/latex]: Successes, [latex]x_2[/latex]
170 80
CALCULATE
Results show in a panel to the right. Test statistic z, p-value, and sample proportions [latex]\hat p[/latex] are displayed.
LibreText Calculator
Go to: Hypothesis Test for a Proportion from the list of online calculators
Enter the following values and press Calculate.
| Sample Size | Number of Successes | |
| First Sample | 240 | 126 |
| Second Sample | 170 | 80 |
| ⭕[latex]\quad\lt[/latex]
🔘[latex]\quad\gt[/latex] ⭕[latex]\quad\ne[/latex] |
CL (confidence level) You can ignore CL entry |
CALCULATE
Results displayed are:
[latex]p[/latex]: p-value
EXAMPLE
Are Republicans just as likely as Democrats to display the American flag in front of their residence on the Fourth of July? 306 of the 593 Republicans surveyed display the flag on the Fourth of July and 327 of the 706 Democrats surveyed display the flag on the Fourth of July. What can be concluded at a significance level of [latex]\alpha = 0.05[/latex]?
SHOW SOLUTION
Is this a test with one sample or two samples?
Since there are two groups (or populations) here and we're trying to compare the flag display rate between the two groups, this is about comparing two proportions. The samples from each population are independent. All of this leads us to a two sample z–test for the difference between two proportions.
Let's label the Republicans as group 1 and the Democrats as group 2.
[latex]p_1 =[/latex] the proportion of Republicans who display the flag on the 4th of July
[latex]p_2 =[/latex] the proportion of Democrats who display the flag on the 4th of July
Sample information
Population 1 (Republicans):
Sample size, [latex]n_1=593[/latex];
Number of successes, [latex]x_1=306[/latex];
Sample proportion, [latex]\hat p_1=\dfrac{306}{593} = 0.5160202360876898[/latex]
Population 2 (Democrats):
Sample size, [latex]n_2=706[/latex] ;
Number of successes, [latex]x_2=327[/latex];
Sample proportion, [latex]\hat p_2=\dfrac{327}{706} = 0.4631728045325779[/latex]
STEP 1: Write the claim (or what's being tested) using mathematical symbols
Republicans just as likely as Democrats [latex]\Rightarrow[/latex] [latex]p_1 = p_2[/latex]
STEP 2: Write the opposite of the claim using mathematical symbols
Opposite of the claim: [latex]p_1 \ne p_2[/latex]. Of the two, the claim is the null hypothesis as it contains the equality sign.
STEP 3: Write the null and alternative hypothesis
The null hypothesis is the statement that contains the condition of equality which in this case is the claim. \[H_0: p_1 = p_2\]\[H_1:p_1 \ne p_2\]
STEP 4: Identify the tail-type of the test and the level of significance, α. If α is not given, assume it to be 5% or 0.05.
This is two-tailed test. Why?
Since the level of significance is given: [latex]\alpha = 0.05[/latex] (or 5% level of significance)
STEPS 5 AND 6:
We're going to use an online calculator to do the heavy lifting of our calculations. Make the selections as shown and calculate the results.
ONLINE CALCULATOR Approach
SUBEDI Calculator
Go to Inference for the Proportion @ rsubedi.com
Number of Samples:
🔲 ONE SAMPLE ✅ TWO SAMPLES
Alternative Hypothesis:
🔲[latex]\quad\lt[/latex] 🔲[latex]\quad\gt[/latex] ✅[latex]\quad\ne[/latex]
Confidence Interval? ← Optional
🔲 Include
Sample Statistics Information:
✅ Successes 🔲 [latex]\hat p[/latex] (p-hats)
Sample Size, [latex]n_1[/latex]: Successes, [latex]x_1[/latex]
593 306
Sample Size, [latex]n_2[/latex]: Successes, [latex]x_2[/latex]
706 327
CALCULATE
Results show in a panel to the right. Test statistic z, p-value, and sample proportions [latex]\hat p[/latex] are displayed.
LibreText Calculator
Go to: Hypothesis Test for a Proportion from the list of online calculators
Enter the following values and press Calculate.
| Sample Size | Number of Successes | |
| First Sample | 593 | 306 |
| Second Sample | 706 | 327 |
| ⭕[latex]\quad\lt[/latex]
⭕[latex]\quad\gt[/latex] 🔘[latex]\quad\ne[/latex] |
CL (confidence level) You can ignore CL entry |
CALCULATE
Results displayed are:
[latex]p[/latex]: p-value
Ignore LB and UB if you did not enter confidence level.
STEP 7: Make the decision by comparing p-value with α
From either of the calculators above, we can obtain the values of the test statistic, z and the p–value. The test statistic, z = 1.8981004323584127 and the p–value = 0.0576828532344833.
Since p–value is greater than or equal to [latex]\alpha[/latex] of 0.05, our decision will be to fail to reject the null hypothesis.
STEP 8: Interpret your decision in the context of original claim
There is insufficient evidence to reject the claim that Republicans are just as likely as Democrats to display the flag on July 4th (i.e. [latex]p_1 = p_2[/latex]).
Interpret the p-value in the context of the study
Assuming the null hypothesis is true, if we were to obtain new samples of the same size as our original ones from each population and compute the difference between new sample proportions, then the probability/chance that the newly obtained difference will be at least as big as the difference we observed in our original samples is called the [latex]p[/latex]–value for two sample cases.
Let's dig a bit into that definition of [latex]p[/latex]–value here:
(1) Assuming the null hypothesis is true: This simply means that if we are to assume [latex]p_1=p_2[/latex], which is the same as saying that there's no difference between the population proportion/percentage of Republicans and Democrats when it comes to flying the flag on July 4th. Note that this assumption is about the equality of population proportions, and not sample proportions.
(2) if we were to obtain new samples of the same size as our original ones from each population and compute the difference between new sample proportions: If we sample another 593 from Republicans and 706 from the Democrats under identical circumstances as what did to obtain our original samples and compute sample proportions for each and calculate the difference.
(3) the probability/chance that the newly obtained difference will be at least as big as the difference we observed: Our original sample proportions were [latex]\hat p_1= \frac{306}{593} = 0.5160202360876898[/latex] for the Republicans and [latex]\hat p_2= \frac{327}{706} = {0.4631728045325779}[/latex] for the Democrats. The difference in sample proportions is [latex]0.05284743155511[/latex]. A positive difference means a higher percentage of __________ display their flags on July 4th while a negative difference means the ____________ have a higher rate. And, the [latex]p[/latex] value of [latex]0.0576828532344833[/latex] tells us that there's about [latex]5.77\%[/latex] chance that if we were to repeat the process, we'll observe a difference of at least [latex]5.28\%[/latex], that is, the observed differences in new samples will be at least as big as [latex]5.28\%[/latex] in magnitude, which is the same as difference in sample proportions we observed in our original samples.
Putting it together:
If the percent of all Republicans who display the American flag in front of their residence on the Fourth of July is the same as the percent of all Democrats who display the American flag in front of their residence on the Fourth of July and if another 593 Republicans and 706 Democrats are surveyed then there would be a 5.77% chance that the percent of the surveyed Republicans and Democrats who display the American flag in front of their residence on the Fourth of July differ by at least 5.28%.
Interpret the level of significance in the context of the study
The significance level [latex]\alpha[/latex] gives us the probability of committing Type I error, which occurs when we throw out a null hypothesis that is true. Any one conducting a study under identical conditions as our original scenario in this question will run a risk of committing Type I error [latex]5\%[/latex] of the time. If a true null hypothesis is rejected in error, that means we'll mistakenly support the alternative hypothesis.
Identical conditions means that the null hypothesis has to be assumed to be true just like we did, and obtain samples of the same size from the populations as we did and run the test exactly like we did. Once again, assuming the null hypothesis is true means that we're assuming that there's no difference in the proportions of the Republicans and Democrats who display their flags on July 4th. If another 593 Republicans and 706 Democrats are sampled, then there will be [latex]5\%[/latex] chance of committing Type I error.
In other words:
If the percent of all Republicans who display the American flag in front of their residence on the Fourth of July is the same as the percent of all Democrats who display the American flag in front of their residence on the Fourth of July and if another 593 Republicans and 706 Democrats are surveyed then there would be a 5% chance that we would end up falsely concluding that the population proportion of Republicans who display the American flag in front of their residence on the Fourth of July is different from the population proportion of Democrats who display the American flag in front of their residence on the Fourth of July.
WORKED OUT EXAMPLE – Testing with Two Samples (VIDEO)
Example using Ti Calculator: Hypothesis Testing With Two Independent Proportions
Practice

